2302. Nuts
for nuts
So
as Ryan and Larry decided that their nuts don't
really taste so good, they realized that there are some nuts located in certain
places of the island, and they love them! Since they’re lazy, but greedy, they
want to know the shortest tour that they can use to gather every single nut!
Can you help them?
Input. The first
line of each test case contains the dimensions of rectangular island x and y (x, y ≤ 20). It is followed by x lines of y characters each as a map of the area, consisting of symbols ‘.’, ‘#’
and ‘L’. Larry and Ryan are currently located in ‘L’. The nuts are represented
by ‘#’. The children can travel in all 8 adjacent directions in one step. There
will be at most 15 places where there are nuts, and ‘L’ will appear only once
on the map.
Output.
Print for each test case on a separate line the minimum number of steps to
gather all the nuts starting from ‘L’, and returning to ‘L’.
|
Sample input |
Sample
output |
|
5 5 L.... #.... #.... ..... #.... 8 10 L......... .......... .......#.. .......... #....#.... .........# .......... ....#..... |
8 23 |
SOLUTION
dynamic programming – travelling
salesman problem
Algorithm analysis
This is a classical traveling salesman problem. You should find a
cycle of minimum length passing through all the vertices of the graph. It
is the same as finding a
Hamiltonian cycle of minimum length. The problem is NP complete and requires
exponential time to solve it with respect to the number of vertices in the
graph.
Let n be the number
of vertices in the graph. For each nut and Larry’s initial location, assign a vertex of
the graph. It follows from the problem statement that n £ 16. All the vertices of the graph will be connected in pairs
(the Euclidean traveling salesman problem is being solved). The length of the
edge connecting the vertices with coordinates (a,
b) and (c, d) is max( |a – c|, |b – d|
). Store the
adjacency matrix of the graph in a two dimensional array m.
It is possible
to generate all possible permutations of numbers from 1 to n using the function next_permutation, each
permutation will correspond to a Hamiltonian cycle. We are looking for the minimum value
among all the lengths of such cycles. The above algorithm requires n! time, which is too much for n = 16 (you should try 16! =
20922789888000 options).
Using the
dynamic programming method, it is possible to solve the problem with O(2n) memory and O(n2 * 2n)
time. For n = 16, there are 16777216 options
should be iterated, which is real
in time.
For a non-empty subset S Í {1, 2, ..., n} and each vertex i Î S, define dp(S, i) as the length of
the shortest path starting at the first (initial) vertex and passing through
all vertices from the set S \ {i} in arbitrary
order and ending at the vertex i. Then the
equalities hold:
dp({1, i}, i) = m[1][i],
dp(S, i) = ![]() (dp(S \ {i}, j) + m[j, i] )
(dp(S \ {i}, j) + m[j, i] )
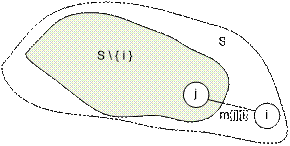
The dp(S, i)
values are recomputed dynamically, memoizing them in array dp. The
Hamiltonian cycle of minimum length is
![]() (dp({1, 2, ..., n}, j) + m[j, 1] )
(dp({1, 2, ..., n}, j) + m[j, 1] )
Example
In the first
test, it is enough to go down the island (4 steps), collecting all the nuts
along the way, and go up to the starting place (4 more steps).
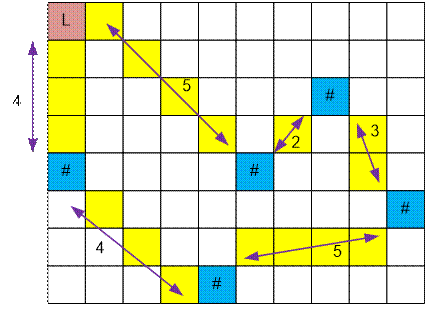
Consider the second test.
Five nuts and Larry’s starting position form a graph of 6 vertices. The figure
shows a Hamiltonian path of length 23.
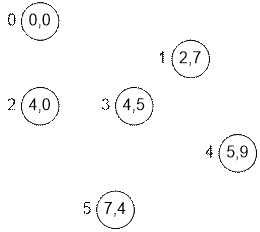
Ñonsider the
computation process in details. Each vertex contains the (x, y) coordinate of the nut to which it
corresponds. Near each vertex its number is indicated.
Initialize dp({0, i}, i) = m[0][i] (vertex 0 is Larry location):
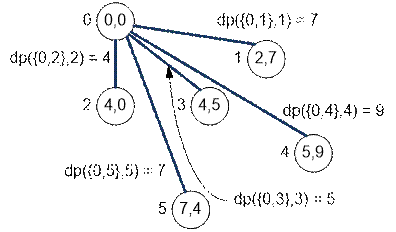
Vertex 0 in the mask corresponds to the least significant
bit. The equality dp({0, i},
i) = m[0][i] is equivalent to dp(2i + 1, i) = m[0][i],
since the set {0, i} corresponds to the mask 2i + 1.
Consider the Hamiltonian
paths along the first three vertices if the path ends at vertex 1 (from the left) or vertex
2 (from the right).
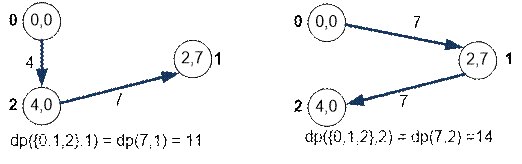
Find the minimum
length of the Hamiltonian path along the first four vertices, which ends at
vertex 3:
dp({0, 1, 2, 3},
3) = min(dp({0, 1, 2}, 1) + m[1][3],
dp({0, 1, 2}, 2) + m[2][3])
=
min(11 + 2, 14 + 5) =
min(13, 19) = 13
The minimum is
attained on the term dp({0, 1, 2}, 1) + m[1][3], therefore the
best way would be
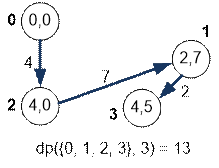
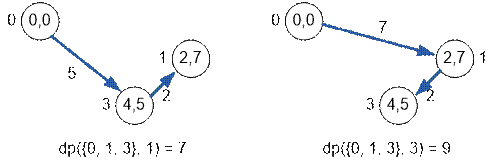
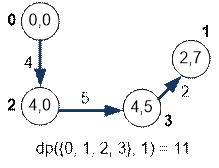
Consider the Hamiltonian
paths along the vertices {0, 1, 3} if the path ends at vertex 1 (from the left) or vertex
3 (from the right).
Find the minimum
length of the Hamiltonian path along the first four vertices, which ends at
vertex 2:
dp({0, 1, 2, 3},
2) = min(dp({0,
1, 3}, 1) + m[1][2],
dp({0, 1, 3}, 3) + m[3][2])
=
min(7 + 7, 9 + 5) = min(14,
14) = 14
The minimum is
attained on both terms; therefore, there are two Hamiltonian paths of the same
length:
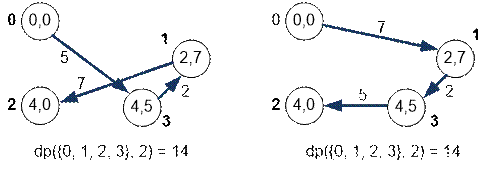
Consider the Hamiltonian
paths along the vertices {0, 2, 3} if the path ends at vertex 2 (from the left) or vertex
3 (from the right).
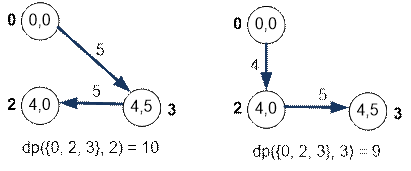
Find the minimum
length of the Hamiltonian path along the first four vertices, which ends at
vertex 1:
dp({0, 1, 2, 3},
1) = min(dp({0, 2, 3}, 2) +
m[2][1],
dp({0, 2, 3}, 3) + m[3][1])
=
min(10 + 7, 9 + 2) = min(14, 11) = 11
The minimum is
attained on the term dp ({0, 2, 3}, 3) + m[3][1], hence the best way is
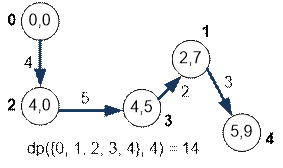
Find the minimum
length of the Hamiltonian path along the first five vertices, which ends at
vertex 4:
dp({0, 1, 2, 3, 4}, 4) = min(dp({0, 1, 2, 3}, 1) + m[1][4],
dp({0, 1, 2, 3}, 2) + m[2][4],
dp({0, 1, 2, 3}, 3) + m[3][4])
=
min(11 + 3, 14 + 9, 13 + 4) =
min(14, 23, 17) = 14
Algorithm realization
Define the
variable INF that equals to infinity,
the maximum possible number of vertices in the graph MAX, and an array dp, where we’ll store the dynamically recomputed values dp(S, i). Each subset S will be stored
as a number, in which the i - th bit
is equal to 1 if the vertex with the number i
is present in it, and zero otherwise. For example, for n = 5, the subset {0, 3, 4} is encoded
with 110012
= 25.
#define INF 100000000
#define MAX 16
int dp[1<<MAX][MAX+1];
Store the map of
the island in the character array mas, the
coordinates of the nuts and the initial position of Larry in arrays x and y, the adjacency matrix of the graph in array m.
int x[21], y[21], m[21][21];
char mas[21][21];
Function solve
computes the value dp(S, last), where the set S is
encoded by the integer mask.
Moreover, S \ {last} equals to mask ^ (1<< last). Next, iterate over all i, i
Î S \ {last} and look for the minimum value res among dp(S \ {last},
i) + m[i][last]. The variable res points to the cell dp[mask][last], so when res changes, the value of dp[mask][last] also changes.
int solve(int
mask, int last)
{
int &res
= dp[mask][last];
if(res ==
INF)
{
mask ^= (1 << last);
for(int i = 1; i < nuts; ++i)
if(mask
& (1 << i)) res = min(res,solve(mask,i) + m[i][last]);
}
return res;
}
The main part of the program.
Read the island’s data into the
array mas, store the coordinates of the nuts into the x and y arrays. Save the initial location of Larry in (x[0], y[0]).
while(scanf("%d
%d\n",&xx,&yy) == 2)
{
for(i = 0; i
< xx; i++) gets(mas[i]);
nuts = 1;
for(i = 0; i
< xx; i++)
for(j = 0; j
< yy; j++)
if
(mas[i][j] == 'L')
{
x[0] = i; y[0] = j;
} else
if
(mas[i][j] == '#')
{
x[nuts] = i; y[nuts++] = j;
}
The number of
graph vertices equal to the number of nuts on the island plus one (Larry initial state)
is stored in the variable nuts. If
there are no nuts on the island, then output 0.
if (nuts ==
1)
{
printf("0\n");
continue;
}
Construct the adjacency
matrix of the graph m. Calculate the
lengths of the edges.
memset(m,0x3F,sizeof(m));
for(i = 0; i
< nuts - 1; i++)
for(j = i +
1; j < nuts; j++)
m[i][j] = m[j][i] = max(abs(x[i] - x[j]),
abs(y[i] - y[j]));
Initially, the
values of dp(S, i) are unknown, set them equal to plus infinity. The set
{0} corresponds to the mask 1, set dp({0}, 0) = 0 (the minimum path from
the zero vertex to it without visiting other vertices is equal to zero). Store the
required minimum cycle length in the variable total.
memset(dp,0x3F,sizeof(dp));
dp[1][0] = 0; total = INF;
Set dp({0, i}, i) = m[0][i] (vertex 0 is Larry location).
for(i = 1; i < nuts; i++) dp[1 | (1
<< i)][i] = m[0][i];
Compute the Hamiltonian
cycle of minimum length. The value 2nuts – 1 corresponds to the set {0,
1, 2, ..., nuts – 1}. Compute the minimum
among all values of dp({0, 1, 2,
..., nuts – 1}, i)
+ m[i][0], 1 £ i < nuts.
for(i = 1; i
< nuts; i++)
total = min(total, solve((1 << nuts)
- 1,i) + m[i][0]);
Print the required minimum cycle length.
printf("%d\n",total);
}